Multi-Scale Simulation

Lesson

Introduction
Random dynamical system
Brownian motion
Multifractal simulation
- Introduction
- Generalizedlimit theorem
- Levy sub-generator
- Multifractal simulation of conservative field
- Fractional integration/differentiation
- Multifractal simulation of non-conservative field
Effect of variation of UM parameters on simulation
To go further
Exercises
Conclusion

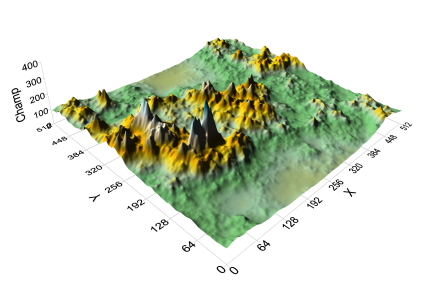
Multifractal simulation of non-conservative field

In the previous paragraph we indicated the different steps leading to construct the continues cascade using the Levy generator for conservative field, with a statistic conservation of the moment of order 1 at the whole scales. For some fields (velocity, passive scalar...) this construction is non valid. Indeed, theses quantities are conserved for moment order different from the unit.

For turbulence studies, the Kolmogorov hypothesis has the generic form:

$\delta \rho_l \approx l^{-H} \varepsilon_{l}^{a}$

Where 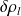is the increment of the non-conservative field over the scale 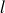, measures the degree of conservativeness, 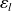is the flux (conservative quantity), and is a dimensional exponent.

The construction of a multifractal non-conservative field is done using the Fractional Integrated Flux (FIF) model proposed by Schertzer et al, 1997. It consists of a fractional integration of conservative flux. This is allows to obtain a distribution equivalent to the one of non conservative field:

$\rho_\lambda (\overline{x}) = \int \limits_{|| \overline{x}|| \in D_\lambda} G(\overline{x}) \varepsilon^{a}_{\lambda} (\overline{x} - \overline{x^{'}}) d\overline{x^{'}}$

This is corresponds to a convolution in physical space of a simple multiplication in Fourier space. Schertzer et al, 1997 demonstrate that has to be a scaling law such as:

$G(\overline{x}) = || \overline{x}||^{-D + H}$

Multifractal non conservative field simulated using the following parameters : alpha = 1.8, C1 = 0.1 and H = 1/3, at the resolution lambda= 512

Homepage