content
menu
navigation
page footer

Multi-Scale Simulation

Lesson

Introduction
Random dynamical system
Brownian motion
Multifractal simulation
- Introduction
- Generalizedlimit theorem
- Levy sub-generator
- Multifractal simulation of conservative field
- Fractional integration/differentiation
- Multifractal simulation of non-conservative field
Effect of variation of UM parameters on simulation
To go further
Exercises
Conclusion

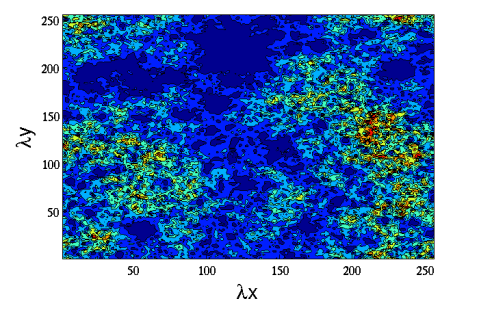
Multifractal simulation of conservative field

The construction of multifractal conservative field at resolution corresponds to a transformation of Levy noise 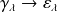. The generator 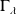is an equivalent process as random walk with Levy increment:

$\Gamma_\lambda (x) = \int g_\lambda (x- x^{'}) \gamma_\alpha (x^{'}) d x^{'}$

Where is the sub-generator, is the kernel. is defined in 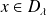, where 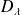is the integration domain 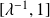, then the kernel 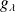is defined as:

$g_\lambda (x) = |x|^{-1/ \alpha}; |x| \in D_\lambda \\$

The integral is just a convolution product which can be expressed as:

$\Gamma_\lambda (x) = g_\lambda (x) \ast \gamma_\alpha (x)$

For multidimensional simulation it is suitable to generate a Levy white noise over the complete domain, then to filter it using a function (kernel). In order to define the kernel we have apply the operator T_\lambda (see Cascade Phenomenology courses) to the integral.

2D numerical simulation of conservative field using : alpha = 1.5 and C1 = 0.03

Created with Scenari (new window)