Generalizedlimit theorem
For a set of
 independent and identically distributed random variables (i.i.d)
independent and identically distributed random variables (i.i.d)
 (
(
 defines the equality in probability distribution) with
defines the equality in probability distribution) with
 , there exists
, there exists
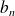 positive and
positive and
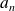 positive such as:
positive such as:
For a Gaussian variable with a finite variance corresponds to :
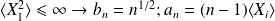 where
where
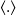 is the ensemble average. The limit
is the ensemble average. The limit
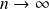 of above sum corresponds to generalized limit theorem:
of above sum corresponds to generalized limit theorem:
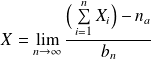
This limit converge to a Gaussian variable
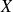 , event if the variables
, event if the variables
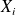 are not Gaussian, bu have a finite variance:
are not Gaussian, bu have a finite variance:
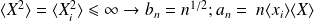 .
.
A generalization of the Gaussian case has been made by Levy (1954) by relaxing the assumption of finite variance by the variables
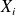 (which means that each statistical moment to the limit is finite). Levy introduced the order of divergence
(which means that each statistical moment to the limit is finite). Levy introduced the order of divergence
 for the moments of the variables
for the moments of the variables
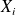 :
:
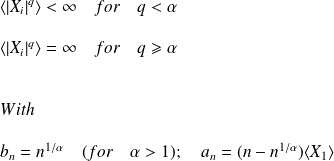
The order of divergence of the moment
 is called the Levy index
is called the Levy index
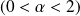 .
.





