Multi-Scale Simulation

Lesson

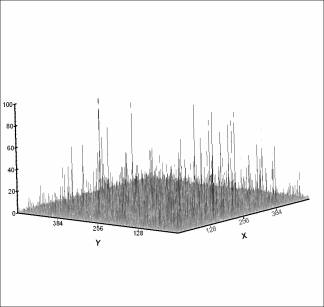
Levy sub-generator

Due to the fact that we want to generate a universal multifractal fields and being the cascade sub-generator is equivalent to a stochastic process with Levy distribution, it will be obtained from a white noise with the parameter and 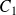. First, we generate a random Levy variable according to the value of , then the amplitudes are modified using 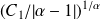in order to obtain the suitable 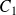. The stochastic noise also called sub-generator is obtained using the method proposed by Chambers et al (1976):

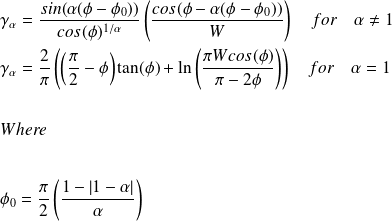
$\gamma_\alpha = \frac{sin(\alpha(\phi - \phi_0))}{cos(\phi)^{1/ \alpha}} \left( \frac{cos(\phi - \alpha(\phi -\phi_0))}{W} \right) \quad for \quad \alpha \neq 1 \\ \quad\\ \gamma_\alpha = \frac{2}{\pi} \left( \left( \frac{\pi}{2} - \phi \right) \tan(\phi) +\ln\left( \frac{\pi W cos (\phi)}{\pi -2 \phi} \right) \right) \quad for \quad \alpha =1\\ \quad\\ \quad\\ Where \\ \quad\\ \quad\\ \phi_0 = \frac{\pi}{2} \left( \frac{1 - |1- \alpha| }{\alpha} \right)$

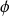is uniform random variable in bounds ( 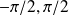) and 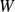is an exponontiel standard variable.

Levy sub-generator using the parameter : alpha = 1.8 and C1 = 0.1 (Macor 2007)

Homepage