Multi-Scale Simulation

Lesson

Fractional integration/differentiation

Fractional integration of order is a generalization of a classical integration, and the fractional differentiation of order is just a generalization of the classical derivation. A fractional integration of order of the function can be obtained using the fractional integral of Rienmann-Liouville:

$I_H g(t) = \frac{1}{\Gamma(H)} \int \limits _{-\infty}^{t} |t - \tau |^{H-1} g(\tau) dt$

One of the easiest way to perform the fractional integration/differentiation is to pass in the Fourier space and just devise/multiply by a non integer power function. Then the above equation consists of a multiplication by .

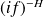The fractional integrations/differentiations correspond to an extension of usual integrations and differentiations at non integer order. There exists several definition of fractional differentiation or integration (see for example Miller and Ross 1993; or Yanvosky et al 2001). In fact the above equation is a special case of a convolution integral:

$I_H g(t) = \int_0^{t} g(\tau) u(t-\tau) dt$

Where

$u(t-\tau) = |t-\tau|^{H-1}$

Homepage