Dynamical Systems

Lesson

Poincaré map

A method that is helpful in analyzing the stability of systems is to take a “snapshot” of the system once per drive cycle. Each snapshot data is plotted as a single point in a standard phase space plot. This type of analysis is called a Poinrcaré map. A Poincaré map can be seen as a discrete dynamical system with a dimension of state space equal to the original continuous dynamic system 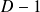. As this new dynamic system retains several properties of periodic and quasi-periodic orbits of the original system and the new system has as a state space of lower dimension, it is often useful for the analysis of the original system. On the other hand, this is not always possible in practice because there is no general method of construction of the Poincaré.

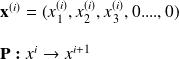
$\textbf{x}^{(i)} = (x_1^{(i)}, x_2^{(i)}, x_3^{(i)},0....,0)\\ \quad\\ \textbf{P : } x^{i} \rightarrow x^{i+1}$

The Poincaré map x → P(x), mapping an intersection x of the trajectory with a hyperplan to the consecutive intersection P(x).

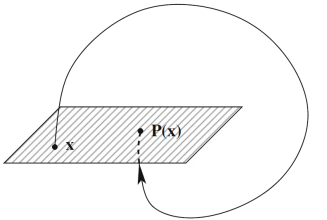
As an illustration of how to represent the Poincaré map for dynamical system, we give the example of Rössler attractor (we will get back later to this point for more explanation).

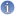The Evolution of a Poincaré map around a Rössler attractor | Information^[1]

https://www.youtube.com/channel/UC0KMlkvE0AgSmecKaLvcGog

Homepage