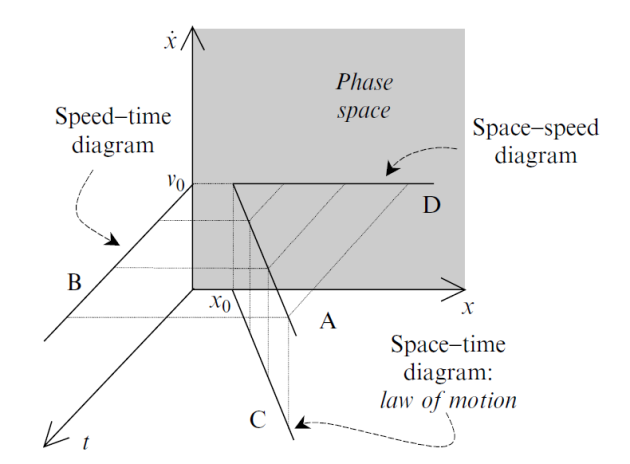
Phase space
Dynamical systems can be described by using the concept of phase space wich can be defined as follows:
A phase space of dynamical system is a theoretical space where every state of system is mapped to a unique spatial location.
The number of state variables needed to uniquely specify the system's state is called the degrees of freedom in the system. We can build a phase space of a system by having an axis for each degree of freedom, i.e., by taking each state variable as one of the orthogonal axes. Therefore, the degrees of freedom of a system equal the dimensions of its phase space. For example, describing the behavior of a pendulum, the axis of its phase space are defined by the angle and the angular velocity.
 Information[1]
Information[1]




