Fixed point
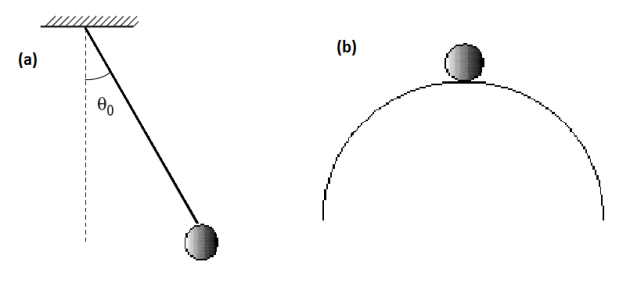
In the theory of complex or nonlinear dynamical systems we find the term fixed point. In the description of dynamical systems, an important objective is the description of the fixed points, or stationary states of the system; these are the values of the variable for which it evolves over time. Some of these fixed points are attractive, which means that if the system succeeds in their vicinity, it will converge to the fixed point. If a mechanical system is in a stable equilibrium state, then a small thrust will result in a localized movement, for example, small oscillations in the case of a pendulum (figure.a). In a system with shock absorber, a stable equilibrium is also asymptotically stable. On the other hand, for an unstable balance, such as a ball resting on a hilltop (figure.b), some small breakouts will result in a greater range of motion that may or may not converge to the original state.
Lets
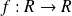a continuously differentiable function with a fixed point
.
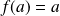. Consider the dynamic system obtained by iterating the function
:
The fixed point is stable if the absolute value of the derivative of
in
is strictly less than 1, and unstable when it is strictly greater than 1.
