Bifurcations
When the behavior of a system depends on one or more factors, the equations that describe the behavior dependent on one or more control parameters. For some values of these control parameters, there is qualitative change in the behavior of the system, corresponding to a change in the number or stability of fixed points. We are dealing with a bifurcation. Generic bifurcations are those that usually take place and not individual cases.
The properties of nonlinear dynamic systems that evolve over time, are closely linked to the evolution of the system equilibrium points. Any change in the number or stability sometimes affects dramatically the behavior of the system. In addition, these changes are made within a few scenarios to outline a classification changes in behavior.
Lets consider the following application:
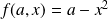, for each control value of
corresponds to a different transformation. The fixed point satisfying
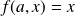are the one that intercept with 2 curves:
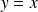and
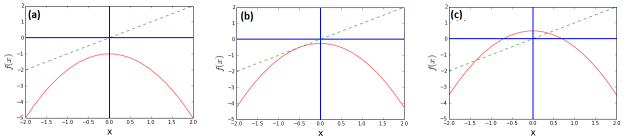
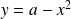. Plotting these curves for 3 values of
we obtain:
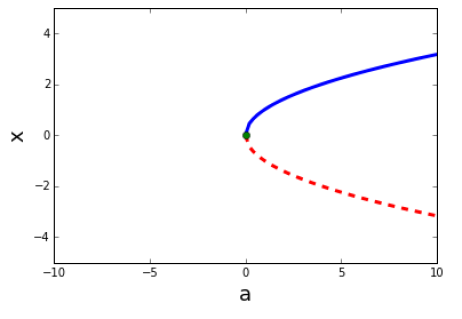
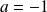there is no intersection, so no fixed point
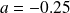the two curves are tangent, there iare two fixed points.
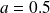there are two fixed points, one of which is is one well (for x> 0) and the other a source, as can be verified by plotting the result of iterated in share cobweb side of the fixed point.
We can draw the bifurcation diagram, carrying the abscissa of fixed points depending on the value of the parameter
