Dynamical system
A dynamic system can be described by a pair
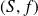 where
where
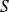 is a nonempty set called also state space and
is a nonempty set called also state space and
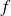 is a function called law of motion from
is a function called law of motion from
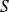 into
into
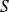 . Thus, if
. Thus, if
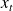 is the state of the system at time
is the state of the system at time
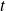 , then
, then
Is the state of the system at time
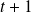 . As examples we can take
. As examples we can take
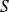 to be the set
to be the set
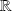 of real numbers, and defined as:
of real numbers, and defined as:
Where
 and
and
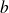 are real numbers. The evolution of the dynamical system
are real numbers. The evolution of the dynamical system
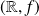 is described by the difference equation:
is described by the difference equation:
Once the initial state
 is defined, one ca write
is defined, one ca write
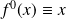 ,
,
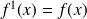 and for every positive integer
and for every positive integer
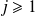 :
:
In the study of the dynamical systems one can define a fixed and periodic points which capture the intuitive idea of stationary or an equilibrium of a dynamical system. A point
 is a fixed point if
is a fixed point if
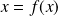 . A point
. A point
 is a periodic point of a period
is a periodic point of a period
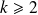 if
if
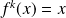 and
and
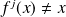 for
for
 .
.
The attractive
 points are a special case of mathematical attractor concept.
points are a special case of mathematical attractor concept.





