Multi-Scale Simulation

Lesson

Markov Processes

Before starting to introduce the random dynamical system, we will speak about a Markov process. In theory and application Markov process is one of the most important classes of stochastic processes. A set of random variables 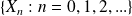with values in a state space 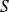is said to be a Markov process if, for each 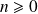, the conditional distribution of , given 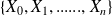depends only on .

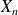The Markov process is characterized by the conditional distribution: 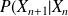, which is also called the probability transition between two process's states. The transition probability for two, three or more steps is obtained from the transition probability of a step, and the Markov property:

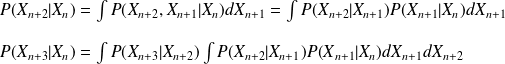
$P(X_{n+2} | X_n) = \int P(X_{n+2},X_{n+1} | X_n) dX_{n+1} = \int P(X_{n+2} | X_{n+1}) P(X_{n+1} | X_{n}) dX_{n+1} \\ \quad\\ P(X_{n+3} | X_n) = \int P(X_{n+3} | X_{n+2}) \int P(X_{n+2} | X_{n+1}) P(X_{n+1} | X_{n}) dX_{n+1} dX_{n+2}$

The Markov processes are widely used in different field:

In physics : The Markovian assumption is when probabilities are used to model the state of a system.

Markov processes are also used bioinformatics to model the relationship between successive symbols in a sequence ( nucleotides for example) , going beyond the polynomial model.

The popularity of a Web page ( PageRank ) as used by Google is defined by a Markov process.

Homepage