Multi-Scale Simulation

Lesson

Introduction
Random dynamical system
- Dynamical system
- Markov Processes
- Random dynamical systems
Brownian motion
Multifractal simulation
Effect of variation of UM parameters on simulation
To go further
Exercises
Conclusion

Random dynamical systems

A random dynamical system is described by a triplet 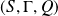where 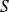is the space state, 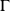is the family of maps from 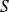into itself (set of all admissible laws of motion) and 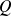is a probability distribution on 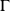. The evolution of the system can be represented as follows: first, the system is in some state in 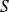, an element 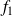from 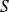is chosen randomly according to the distribution 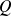, and the system moves to the state 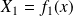. Anew, 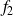is chosen independently of 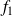from 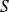according 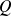such as .

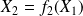On some probability space, let 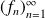be a sequence of random functions from 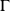with a common distribution 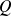. For a given random variable 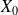, independent of the sequence 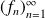, define

$X_1 \equiv f_1(X_0) \equiv f_1X_0 \\ \quad \\ X_{n+1} = f_{n+1} (X_n) \equiv f_{n+1}f_{n}...f_{1} X_{0} \quad (n \geq 0)$

Then 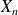is a Markov process with a stationary transition probability 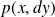given as follow: for , :

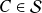$p(x, C) = Q( \{ \gamma \in \Gamma : \gamma(x) \in C \})$

Homepage