Brownian Motion equation
The Brownian Motion, named in honor of the botanist Robert Brown, describes the motion of particle subjected to an infinity of shocks in very short time, and its and its trajectories are irregular. They have the following proprieties:
The trajectory of the particle at the time prior of
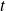does not acts on the future trajectories. This propriety is called a Markov propriety.
The particles move continuously in space.
The law of the position of the particle between two instants
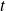and
depends only on
. The increases are then stationary.
If
denotes the position of the particle at the time
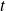, and due to the previous proprieties it is easy to show that
follows a normal distribution , with zero mean and a variance
.
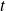For a short time scale, the particles are pushed in some direction, this implies that the average position at the time
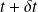knowing the position
is given by
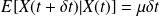for a vector
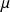, which can also depends on
. We can write :
Where
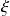is a normal Gaussian centered covariance identity. It is easy to check that:
![E[X(t + \delta t) | X(t)] = \mu \delta t\\ \quad \\ And \\ \quad\\ E[ (X(t + \delta t)- E[X(t + \delta t) | X(t)] )^2] = \sigma (X(t)) \sigma (X(t))^T \delta t](../res/eq6.png)
Where
is a matrix-valued function (which is not necessarily a square matrix), and
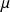a vector-valued function.
