Multi-Scale Simulation

The deterministic equation described above is valid only if the mass of the particle is large so that its velocity due to thermal fluctuations is negligible. From the equipartition law, the mean energy of the particle is:

where id the Boltzmann's constant and 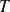is the temperature. Assuming the mass of particle is larger than the mass of molecules, the deterministic equation which describe the motion of the particle is still valid but we have to add the fluctuating force 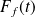on the right-hand side. The total force acting on the small particle is:

The stochastic force occurs because we are dealing with large number of molecules in fluid and we can not define their initial values. As usually done in thermodynamics, we can consider an ensemble of such systems (Gibbs ensemble). The force 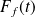then varies from system to system and the only thing we can do is to consider averages of this force for the ensemble. The motion of the molecules does not being known in details, the rhs of the above equation can be modeled by random force or a noise. The way to model the noise depends on the nature of the fluid in which the molecules are and the characteristic time/length scale. The simplest configuration arises when the decorrelation time of molecules is negligible compared the characteristic time scale of the particle, this is called white noise. It is mathematically modeled by a Brownian Motion or Wiener Process.