Continuous cascade
In the previous lecture we discuss and practice the discrete in scale models constructed by iteratively dividing large structures (eddies) into disjoint daughter sub-eddies each reduced in scale by an integer ratio
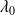. These cascade have significant limitations, the fact that such cascade are developed only on a countable set of scales (hence the name discrete cascades). We have seen that this limitation can be supported using the continuous cascade. During this exercise we will simulate a continuous multifractal field with different sets of UM parameters.
Question
Write a main code which calls the following function in order to generate a multifractal field with
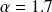and
.
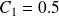Play with different values of the UM parameter to generate different field and comment the obtained result.
// Generate a Levy variable
function [L] = Levy(alpha, lambda)
L = zeros(1,lambda);
for i = 1:lambda
U = rand();
W = exp(-U);
a = - %pi/2; b = %pi/2;
Phi = a + (b-a).*rand();
Phi0 = -(%pi/2)*(1-abs(1-alpha))/alpha;
L(i) = sign(alpha-1)*sin(alpha*(Phi-Phi0))*cos(Phi)^(-(1/alpha))*(cos(Phi-alpha*(Phi-Phi0))/W)^((1-alpha)/alpha);
end
endfunction
function [Y]= ColorFunc(L, lambda, alpha)
ap = (alpha/(alpha-1));
// FFT
X = fft(L);
N = lambda/2 + 1;
n = 1:N;
X(1:N) = X(1:N).*(n.^(-1/ap));
X(N+1:lambda) = real(X(lambda/2:-1:2)) -%i*imag(X(lambda/2:-1:2));
Y = ifft(X);
Y = real(Y(1,1:lambda));
endfunction
// Continuous simulated field
function [Sim]=Continuous(alpha,C1,lambda)
l = Levy(alpha, lambda);
L = l.*((C1/(alpha-1))^(1/alpha));
Gamma = ColorFunc(L,lambda,alpha);
Generator = exp(Gamma);
Sim = Generator./(lambda^(C1/(alpha-1)));
endfunction
clear;
clc;
exec("Levy.sce");exec("FracIntegration.sce");exec("ColorFunc.sce");exec("Continuous.sce");// Universal multifractal parameters
alpha = 1.7;
C1 = 0.5;
lambda = 2^12;
// Continuous simulation
Sim = Continuous(alpha,C1,lambda);
