Spectral Analysis

Lesson

Introduction
Some definitions
Power spectral density (PSD)
Scaling analysis
- Spectral exponent
- Scaling analysis : anisotropy
- Scaling analysis : boundary layer
Identification of some processes
Exercises
To go further
Conclusion

Spectral exponent

The symmetries of the governing equations developed in the previous courses (see source of complexity courses) can be used in order to perform the theoretical expression of spectral exponent β.

In the case of turbulence, considering the energy flux :

$\varepsilon = \frac{- \partial v^2}{\partial t}$

Where 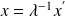and

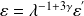
If it is scale invariant 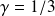, hence Kolmogorov 1941^[1] derived the first scaling law :

$\Delta v \approx \varepsilon^{1/3} \Delta x^{1/3}$

A similar scaling analysis in Fourier space yields to the famous 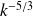derived by Obukhov 1941 :

$E(k) \approx \varepsilon ^{2/3} k^{-5/3}$

Kolmogorov, A. N, [1941]
Kolmogorov, A. N. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In Dokl. Akad. Nauk SSSR (Vol. 30, No. 4, pp. 301-305).

Homepage