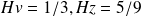Spectral Analysis

Lesson

Introduction
Some definitions
Power spectral density (PSD)
Scaling analysis
- Spectral exponent
- Scaling analysis : anisotropy
- Scaling analysis : boundary layer
Identification of some processes
Exercises
To go further
Conclusion

Scaling analysis : anisotropy

The same scaling analysis can be conducted in the case of anisotropy. We will see that the effect of the gravity and Coriolis forces add some complexity to the analysis. The governing equations :

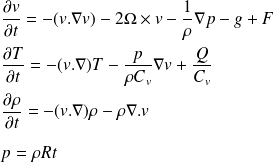
$\frac{\partial v}{\partial t} = - (v.\nabla v) - 2 \Omega \times v - \frac{1}{\rho} \nabla p - g + F\\ \quad \\ \frac{\partial T}{\partial t} = - (v.\nabla)T - \frac{p}{\rho C_v} \nabla v + \frac{Q}{C_v}\\ \quad \\ \frac{\partial \rho}{\partial t} = - (v.\nabla) \rho - \rho \nabla . v\\ \quad \\ p = \rho Rt$

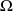Is the earth rotation, 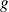is the gravity, 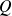represents the source and the sink of energy, is the universal gas constant 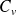is the specific heat constant.

The detail of the scaling analysis in the case of anisotropy can be found in [Lovejoy and Schertzer, 2014]^[1], where :

Lovejoy, S., & Schertzer, D, 2014
Lovejoy, S., & Schertzer, D. (2013). The weather and climate: emergent laws and multifractal cascades. Cambridge University Press.

Homepage