Cascade phenomenology

Lesson

Introduction
The matter of scale
Intermittency
Discrete cascade
- Introduction
- Cascade principle
- β-model
- α-model
- p-model
Other type of cascade
Exercises
To go further
Conclusion

α-model

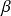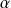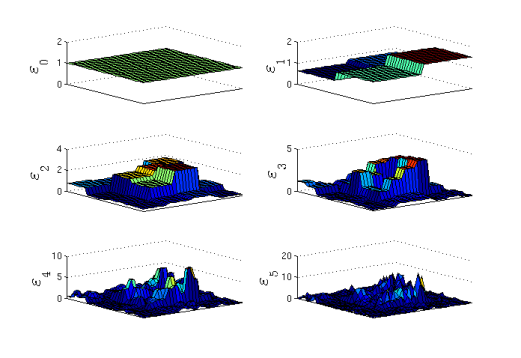
While the model assign to the structure one of the two states "dead" or "alive", the model ([Schertzer, D., and Lovejoy, S, 1984]^[1]) lets say such structure is more or less active. The 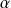model ()process distribute randomly the occurrence weight to each structure of a given generation. It is obey of Bernoulli's process such as :

$\begin{eqnarray*} Pr(\mu_{\varepsilon} = \lambda^{\gamma_+}) = \lambda^{-c} \quad ( >1 \quad Increase) \\ Pr(\mu_{\varepsilon} = \lambda^{\gamma_-}) =1- \lambda^{-c} \quad (<1 \quad Decrease) \end{eqnarray*}$

2D field generated using α-model cascade

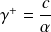Where : and ;

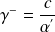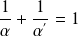
For ensemble conservation : 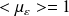, which implies that : .

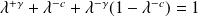Where 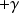and 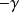are the singularities.

[Schertzer, D., and Lovejoy, S, 1984]
Schertzer, D., & Lovejoy, S. (1984). Elliptical turbulence in the atmosphere. In Symposium on Turbulent Shear Flows, 4 th, Karlsruhe, West Germany (p. 11).

Homepage