Cascade phenomenology

β-model

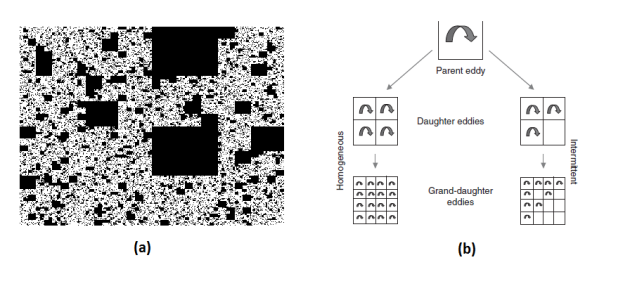
The simplest cascade model is the 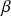-model ([Novikov, E. A., & Stewart, R. W. 1964][1], [Frisch, U et al, 1978][2]). This model takes into account the intermittency of the studied field by assigning two possible states, than the generated structures can be "alive" or "dead". The random variable 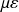follow a binomial law as :

\begin{eqnarray*} Pr(\mu = 0) = 1 - \lambda^{-c} \quad (dead) \\ Pr(\mu = \lambda^{-c}) = \lambda^{-c} \quad (alive) \end{eqnarray*}
(a): 2D field generate using β-model, (b) : A schematic diagram showing the first few steps in a cascade process [Lovejoy and Shertzer]InformationInformation[3]

The 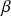-model is very caricatural of some physical process, However, it is an excellent pedagogical case to introduce de cascade phenomenology.

  1. [Novikov, E. A., & Stewart, R. W. 1964]

    Novikov, E. A., & Stewart, R. W. (1964). The intermittency of turbulence and the spectrum of energy dissipation fluctuations. Izv. Geophys. Ser, 3, 408-413.

  2. [Frisch, U et al, 1978]

    Frisch, U., Sulem, P. L., & Nelkin, M. (1978). A simple dynamical model of intermittent fully developed turbulence. Journal of Fluid Mechanics, 87(04), 719-736.

  3. (b): Lovejoy, S., & Schertzer, D. (2013). The weather and climate: emergent laws and multifractal cascades. Cambridge University Press.

PreviousPreviousNextNext
HomepageHomepagePrintPrintCreated with Scenari (new window)