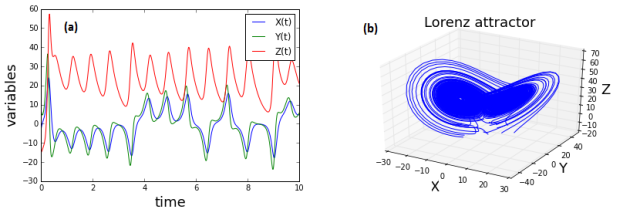
Lorenz Attractor
The resulting equations for the time dependent parameters of the approximate Lorenz convection equations are
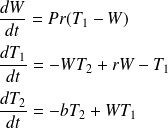
Where
with the critical Rayleigh number
Question
1 - Identify
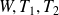as
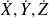and write a python (or another programming language ) to solve the time evolution of the three variables.
2 - Change
to 10, and then 24. Plot the time evolution of the variables and comment on how these solutions differ.
Solution
1
"""2
@author: yacine.mezemate3
"""4
from __future__ import division
5
6
import numpy as np
7
from scipy.integrate import odeint
8
import matplotlib.pyplot as plt
9
from mpl_toolkits.mplot3d import Axes3D
10
11
from matplotlib.colors import cnames
12
13
14
15
# System of differential equations16
def LorenzSystem((x,y,z), t0, sigma=10., beta=8./3, rho=28.0):
17
return [sigma*(y-x), x*(rho-z)-y, x*y -beta*z]
18
19
#Initial condition20
np.random.seed(1)
21
x0 = -15 + 30 * np.random.random((30, 3))
22
23
# Time 24
t = np.linspace(0, 10, 1000)
25
26
#System resolution27
x_t = np.asarray([odeint(LorenzSystem,x0i,t) for x0i in x0])
28
29
30
# Plots31
fig = plt.figure()
32
ax = fig.add_subplot(111, projection='3d')
33
for i in range (0,29):
34
ax.plot_wireframe(x_t[i,:,0],x_t[i,:,1],x_t[i,:,2])
35
plt.title("Lorenz attractor", fontsize =18)
36
ax.set_xlabel('X', fontsize =18)
37
ax.set_ylabel('Y', fontsize =18)
38
ax.set_zlabel('Z', fontsize =18)
39
40
plt.figure(2)
41
plt.plot(t,x_t[0,:,0], label="X(t)")
42
plt.plot(t,x_t[0,:,1], label="Y(t)")
43
plt.plot(t,x_t[0,:,2], label="Z(t)")
44
plt.xlabel("time", fontsize=18)
45
plt.ylabel("variables", fontsize =18)
46
plt.legend()
47
plt.show()
48
49
