Dynamical Systems

Lesson

Introduction
Introduction to dynamical systems
Non-linear dynamical system
Bifurcations and routes to the chaos
Chaos
Exercises
- Quiz: Linear dynamical system
- Quiz: Non-Linear dynamical system
- Quiz: Lorenz Attractor
To go further
Conclusion

Linear dynamical system

The equation of motion for the pendulum is found by equating the mass times acceleration of the pendulum bob to the component of the force acting on the bob – its weight – along the direction of motion. The bob moves on the arc of a circle of radius 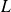, and the distance traveled along the tangent to the arc is denoted, 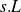is the length of the pendulum.

Question

1 - Set the governing equation

2 - Write a program to solve the obtained differential equation.

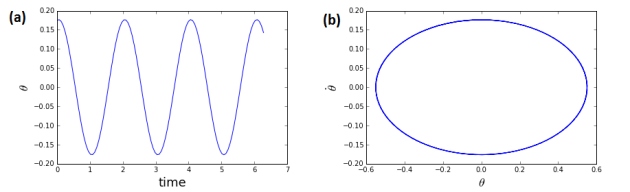
3 - Plot the time evolution of the angle 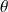and represent the corresponding phase space.

Solution

"""
@author: yacine.mezemate
"""
import numpy as np
from math import *
from scipy.integrate import odeint
import matplotlib.pyplot as plt
g = 9.81
L = 1
theta0 = (10*2*pi)/360
omega0 = 5*2*pi/360
x0 = np.array([theta0, omega0])
t = np.linspace(0,pi*2,100)
global k, damping_force
damping_force = 0
k = g*L
def SystemEquation((x1,x2), t0):
    return [x2, -k*sin(x1) -damping_force*x1]
    
x_t = odeint(SystemEquation, x0, t)
plt.figure(1)
plt.plot(t,x_t[:,0])
plt.ylabel(r"$\theta$", fontsize=18)
plt.xlabel(r"time", fontsize=18)
plt.show()
plt.figure(2)
plt.plot(x_t[:,1], x_t[:,0])
plt.ylabel(r"$\dot{\theta}$", fontsize=18)
plt.xlabel(r"$\theta$", fontsize=18)
plt.show()

"""
@author: yacine.mezemate
"""
import numpy as np
from math import *
from scipy.integrate import odeint
import matplotlib.pyplot as plt

g = 9.81
L = 1
theta0 = (10*2*pi)/360
omega0 = 5*2*pi/360

x0 = np.array([theta0, omega0])
t = np.linspace(0,pi*2,100)

global k, damping_force
damping_force = 0
k = g*L

def SystemEquation((x1,x2), t0):

    return [x2, -k*sin(x1) -damping_force*x1]
    


x_t = odeint(SystemEquation, x0, t)

plt.figure(1)
plt.plot(t,x_t[:,0])
plt.ylabel(r"$\theta$", fontsize=18)
plt.xlabel(r"time", fontsize=18)
plt.show()

plt.figure(2)
plt.plot(x_t[:,1], x_t[:,0])
plt.ylabel(r"$\dot{\theta}$", fontsize=18)
plt.xlabel(r"$\theta$", fontsize=18)
plt.show()

Homepage