Dynamical Systems

Lesson

Introduction
Introduction to dynamical systems
Non-linear dynamical system
Bifurcations and routes to the chaos
- Introduction
- Saddle-Node Bifurcation
- Pitchfork Bifurcation
- Hopf Bifurcation
Chaos
Exercises
To go further
Conclusion

Hopf Bifurcation

A Hopf bifurcation typically causes the appearance (or disappearance) of a limit cycle around the equilibrium point. A limit cycle is a cyclic, closed trajectory in the phase space that is defined as an asymptotic limit of other oscillatory trajectories nearby.

As an example, a dynamical model of a nonlinear oscillator, called the Van der Pol oscillator:

It corresponds to a second differential equation and as mentioned above, this can be solved by introduction an additional variable 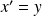, then we obtain the following system of equation:

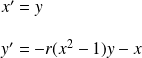
$x' = y \\ \quad \\ y' = -r(x^2 -1)y -x$

The solution of this system can be plotted in the phase space as following:

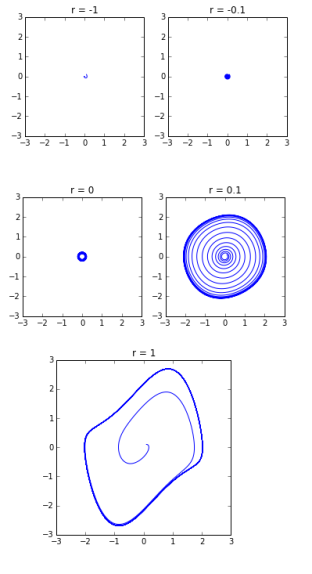
Phase space of Hopf bifurcation for different values of r

The figure shows the results where a clear transition from a stable spiral focus (for 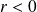) to an unstable spiral focus surrounded by a limit cycle (for 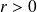) is observed.

Homepage