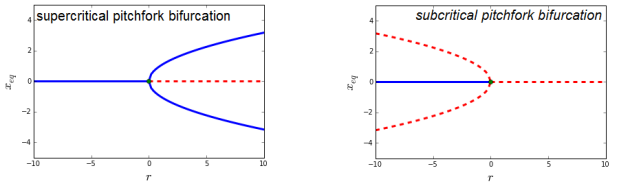
Pitchfork Bifurcation
It is the bifurcation associated with the differential equation:
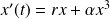. For
the bifurcation is said super-critical and the corresponding equilibrium points are
and the last two point exist only for
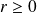. We can show that
is table for
and unstable for
(as shown in the following figure), while
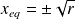are always stable if they exist.
If
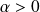, the corresponding equilibrium points are x_{eq} = 0, \pm \sqrt{-r}, but the last two exist only if
. The bifurcation is said sub-critical.
