Dynamical Systems

Lesson

Introduction
Introduction to dynamical systems
- Linear dynamical systems
- First order differential equation
- Second order differential equation
- Linearization
- Limitations of linear systems
Non-linear dynamical system
Bifurcations and routes to the chaos
Chaos
Exercises
To go further
Conclusion

Second order differential equation

There exists several systems (mechanics, chemistry, biology, electricity...etc.) whose behavior can be described using second order differential equation.

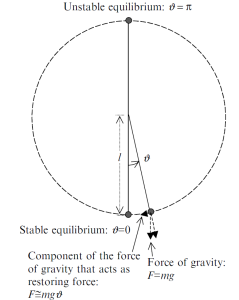
One of the best known examples which is described by a second order differential equation is the oscillation of pendulum.

The equation of the motion of the pendulum is obtained according to

the second law of dynamics (see Source of Complexity module) :

Diagram of pendulum that makes small oscillations in the absence of frictions.

$\begin{eqnarray*} ml \ddot{\theta}(t) = -mg \theta (t) \\ \theta(t) = \theta_{0} cos \omega t \end{eqnarray*}$

The above equation is a homogenous linear differential equation with constant coefficients, whose integration leads to a combination of exponential in a complex field, which translates into simple sinusoidal oscillatory dynamics.

Bertuglia, C. S., & Vaio, F. (2005). Nonlinearity, chaos, and complexity: the dynamics of natural and social systems. OUP Catalogue.

Homepage