First order differential equation
The first special case of first order differential equations that we will look is the linear first order differential equation. This equation can be used to describe in biological field in order to characterize the growth of some population. Indeed, biologists frequently ask the following question:
What will be the population of this animal species in in some time?
How are we protecting the resources from extinction?
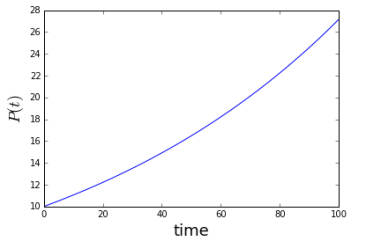
In this lecture we will not answer directly these equations, but we illustrate the use of differential equation. The rate of change of the population is proportional to the existing population. In other worlds if
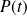measures the population, its rate of changes is given as:
Where the rate
is constant, and if
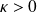we have growth, and if
we have decay. This linear equation is solved to:
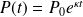. Where
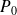corresponds to the initial population
.
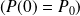