Non-linearity
Chemical kinetics
The laws of chemical kinetics can be written in the form of differential equations. In the case of complex reactions involving several molecules, equations are non-linear. We study the Brusselator model involving 3 substances. The chemical reactions can be translated to differential equation such as:
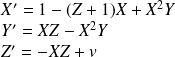
Where
represents the speed of the reaction
Question
Solve numerically the system for different values of
: 0.9, 1.3, 1.52
Hint
For the resolution you can use: Python: Odeint function from scipy module. Or Matlab: ode45
Solution
1
# -*- coding: utf-8 -*-2
'''3
@author: yacine.mezemate4
'''5
6
import numpy as np
7
import matplotlib.pyplot as plt
8
from scipy.integrate import odeint
9
10
global v # Speed reaction
11
12
#v= 0.9 # stable13
v = 1.3 # instable
14
15
U0 = np.array([1,2,1]) # initial condition
16
time = np.linspace(0,60,600) #time
17
18
# System of equation19
#======================================================20
def MySystem(x,t):
21
22
global v
23
Xprim = 1+ np.power(x[0],2)*x[1] -((x[2] +1)*x[0])
24
Yprim = x[2]*x[0] - np.power(x[0],2)*x[1]
25
Zprim = -x[0]*x[2] + v
26
return [Xprim, Yprim, Zprim]
27
#======================================================28
29
# Resolution 30
sol = odeint(MySystem,U0, time)
31
32
# Plot solution33
plt.figure(1)
34
plt.plot(time,sol[:,0], label ="X(t)")
35
plt.plot(time,sol[:,1], label ="Y(t)")
36
plt.plot(time,sol[:,2], label ="Z(t)")
37
plt.legend(loc='down left')
38
plt.title("Evolution of X,Y,Z in time", fontsize=18)
39
plt.ylabel("X(t),Y(t),Z(t)", fontsize =14)
40
plt.xlabel("time", fontsize =14)
41
plt.show()
42
43
plt.figure(2)
44
plt.plot(sol[:,0], sol[:,1])
45
plt.title("Y according X", fontsize=18)
46
plt.ylabel("Y(t)", fontsize =14)
47
plt.xlabel("X(t)", fontsize =14)
48
plt.show()
49
50
Question
For each case, plot the evolution of the concentration in time and the concentration according to others.
Solution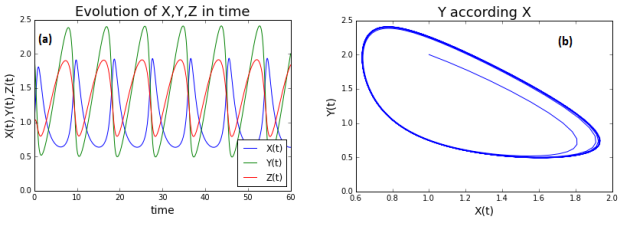
(a): time evolution of the concentration; (b): concentration of molecules Y according to the concentration of molecule X for v =.3
