Source Of Complexity

Lesson

Introduction
Matter of scale
Variability
Non-linearity
Introduction to differential equations
Governing equations
Different approaches
Exercises
- Quiz: Differential equations
- Quiz: Non-linearity
- Quiz: Governing equations
To go further
Conclusion

Differential equations

Classification

Consider the following differential equations:

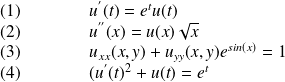
$(1) \quad \quad \quad \quad u^{'}(t) = e^t u(t) \\ (2) \quad \quad \quad \quad u^{''}(x) = u(x) \sqrt{x} \\ (3) \quad \quad \quad \quad u_{xx}(x,y) + u_{yy}(x,y) e^{sin(x)} =1 \\ (4) \quad \quad \quad \quad (u^{'} (t)^2 + u(t) = e^t\\$

Question

Characterize these equations as:

PDES or ODEs

Linear or non-linear

Solution

PDEs: Equation (3)

ODEs: Equations (1), (2)

Linear: Equations (1), (2), (3)

Non-linear: Equation (4)

Cauchy's problem

$\begin{tabular}{lll} $u' = -2u + t^2 -3t$ & & $(sint)u' = (cost)u-1$ \\ u(0) = 1 & & u(0) = 1 \end{tabular}$

Question

Solve the above Cauchy's problems for

Solution

Lets begin with the first (left) problem. The general solution of the homogenous equation is 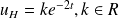. A particular solution of a non-homogenous equation can be found as by identification we can found 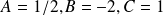. Then, the general solution of the non homogenous equation is

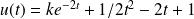
Question

Are the solutions unique ?

Solution

When we substitute one can found the solution of the Cauchy's problem : , this solution is unique in because the function 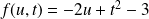is Lipshitz.

Homepage