Introduction
The difference between the classical statistics and the extreme value theory is that the former focus on the average behavior of the stochastic process, while the later focus on extreme and rare events.
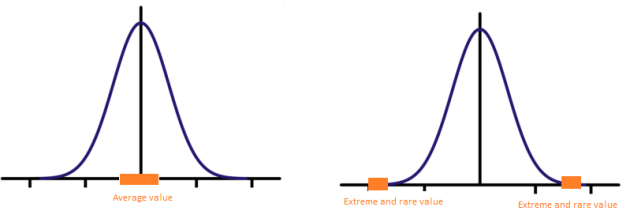
We can found in literature several techniques to study the extreme and rare events:
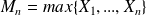for
→
fo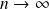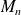llows a Generalized Extreme Value (GEV) distribution.
for very large threshold
→ follows a Peak Over Threshold (POT).
Poisson-Point GPD Process combines POT and Poisson point process
We can define the survival function as
, where
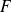is the cumulative distribution function. The extreme values theory was founded to solve two further problems:
To estimate the tail of the survival function: given
, estimate
with
To estimate the extreme percentiles: given
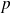estimate
such as
with
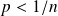i.e estimate
