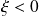Extremes

Lesson

Introduction
Theory
Extreme value theory
- Introduction
- Generalized Extreme Value
- Asymptotic distributions of the maximum
- Conditional distribution of the excesses
- Extreme quantities : level of return
- Hill estimator
Multifractal phase transition
To go further
Exercises
Conclusion

Asymptotic distributions of the maximum

Starting from 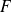on can define the law of maximum 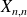as:

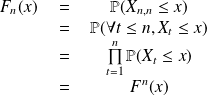
$\begin{tabular}{ccc} $F_n(x) $ & = & $\mathbb{P}(X_{n,n} \leq x)$\\ & = & $\mathbb{P}(\forall t \leq n , X_{t} \leq x)$ \\ & = & $ \prod \limits_{t=1}^{n} \mathbb{P}( X_{t} \leq x)$\\ & = & $F^{n}(x)$ \end{tabular}$

If there exist a constants 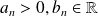and a non-degenerate distribution 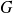such as:

$\lim \limits_{n \rightarrow \infty} \frac{X_{n,n} - a_n}{b_n} \overset{\ell}{\rightarrow} G(x) ; \forall x \in \mathbb{R}$

Then 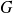is define as:

$G_{\mu, \sigma, \xi}(x) = \left\{ \begin{array}{ll} exp\{ - [1 + \xi(\frac{x - \mu}{\sigma} )]_{+}^{1/\xi} \} \quad if \quad \xi \neq 0\\ exp\{ - exp[ (- \frac{x - \mu}{\sigma} )_{+}] \} \quad if \quad \xi = 0 \end{array} \right. Where \quad x_+= max(0,x)$

Where 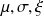are respectively the parameters of: location, scale and the shape of the model. Replacing in 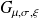the variable 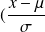by we obtain the standard shape of the distribution of the extreme values (GEV :Generalized Extreme Value):

$G_{\mu, \sigma, \xi}(x) = \left\{ \begin{array}{ll} exp\{ - [1 + \xi x]_{+}^{1/\xi} \} \quad if \quad \xi \neq 0\\ exp\{ - exp[ (-x )_{+}] \} \quad if \quad \xi = 0 \end{array} \right.$

We say that 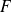is in the attraction domain of:

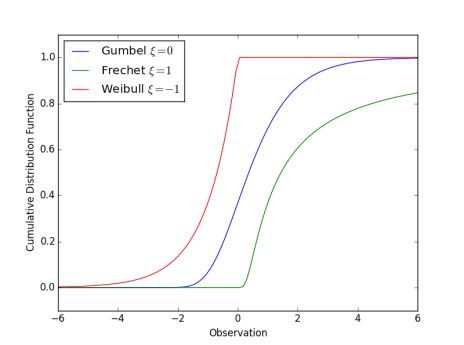
Gumbel if

Fréchet if

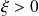
Weibull if

Representation of the cumulative distribution function: Gumbel \xi = 0, Fréchet \xi = 1, Weibull \xi = -1

Homepage