Extremes

Lesson

Introduction
Theory
Extreme value theory
- Introduction
- Generalized Extreme Value
- Asymptotic distributions of the maximum
- Conditional distribution of the excesses
- Extreme quantities : level of return
- Hill estimator
Multifractal phase transition
To go further
Exercises
Conclusion

Conditional distribution of the excesses

The second part of EVT is called the POT method (Peak Over Threshold) consists to use the observations that exceed a certain deterministic threshold and especially the differences between the observations and the threshold, called excess.

Let 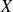a random variable with a CDF 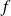and which is a real enough large, called threshold. We define the excess over the threshold the set of random variables 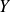such as:

$y_i = x_i - u, \quad x, > u$

We look from the distribution 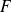of 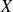to define a conditional distribution with respect to for the random variable exceeding the threshold. We can define the conditional distribution of the excess such as:

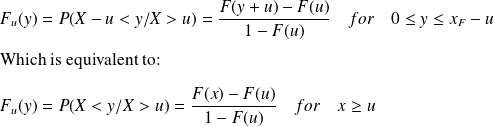
$F_u(y) = P(X-u < y/X >u) = \frac{F(y+u) - F(u)}{1 - F(u)} \quad for \quad 0 \leq y \leq x_F -u \\ \quad \\ \text{Which is equivalent to:}\\ \quad \\ F_u(y) = P(X < y/X >u) = \frac{F(x) - F(u)}{1 - F(u)} \quad for \quad x \geq u$

This method allows to determine by which PDF that we can fit the conditional distribution of excesses when the threshold tends to the point .

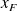Lets the conditional distribution of cumulative distribution function 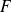with respect to a threshold . When the threshold tends to the value :

$\lim \limits_{u \rightarrow x_F} sup |F_u(y) - H(y)| = 0, \quad 0 \leq y \leq x_F -u$

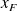The conditional distribution converges to the function 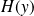which corresponds to the Generalized Pareto cumulative distribution noted GPD. Generalized Pareto law is written as:

$H(y) = 1 + \log G(y)$

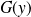corresponds to Generalized Extreme Value law. For 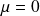(location parameter) the GPD law can be written as:

$H_{\sigma, \xi}(y) = \left \{ \begin{array}{l} 1-\Big(1+ \xi \frac{y}{\sigma}\Big)^{-\frac{1}{\xi}} \quad if \quad \xi \neq 0 \\ \quad \\ 1 - exp(- \frac{y}{\sigma}) \quad if \quad \xi = 0 \end{array} \right.$

Homepage