Empirical power law estimation
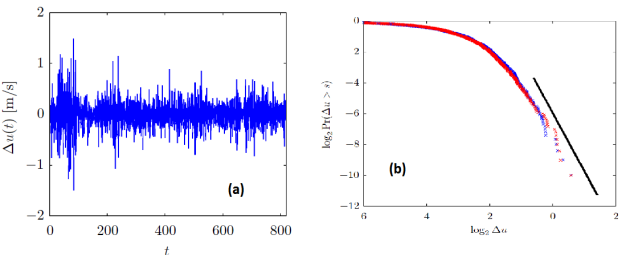
To quantify the behavior of the extremes of a distribution is to try to t a power law of fit the heavy tail(s). We can estimate the exponent by taking the linear regression of the same probabilities versus
 however in a log-log plot. In the following figure we estimate the tail of the distribution of the wind velocity increment, the corresponding divergent moment is
however in a log-log plot. In the following figure we estimate the tail of the distribution of the wind velocity increment, the corresponding divergent moment is
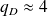 .
.
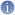 Information[1]
Information[1]The second example shows the predicted power-law behaviour for nondimensional raindrop distributions for which

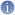 Information[2]
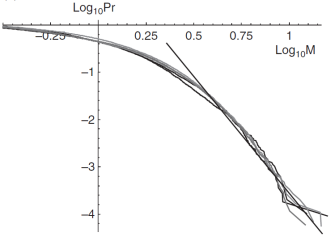
Information[2]