Extremes

Lesson

Introduction
Theory
Extreme value theory
Multifractal phase transition
- Introduction
- Bare and Dressed quantities
- First order phase transition
- Empirical power law estimation
To go further
Exercises
Conclusion

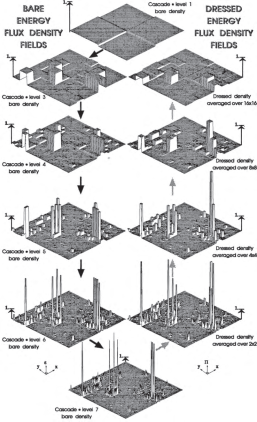
Bare and Dressed quantities

According to the multifractal framework, it is possible to drive a continuous distribution relation between the probability of exceedence of conservative quantity (flux density) and the co-dimension function defined in the lesson Multi-scale Analysis: Multifractal : 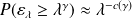. Where 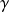represents the singularity and 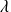the resolution. The question that we can pose is What are the consequences of the singular behavior when ?

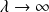This leads to the fundamental difference between the bare and dressed cascade properties; the former have all moments finite whereas the latter will generally have divergence for all moments greater than a critical value .

The terms bare and dressed are borrowed from renormalization jargon and are justified because the bare quantities neglect the small-scale interactions ( ) whereas the dressed quantities take them into account.

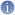The left-hand side shows the step-by-step construction of a (“bare”) multifractal cascade starting with an initially uniformunit flux density. The right-hand side shows step the horizontal scale is divided by 2, and independent random factors are chosen either < 1 or > 1. Wilson et al. (1991) | Information^[1]

The left-hand side shows the step-by-step construction of a (“bare”) multifractal cascade starting with an initially uniformunit flux density. The right-hand side shows step the horizontal scale is divided by 2, and independent random factors are chosen either < 1 or > 1. Wilson et al. (1991) | Information^[1]

Wilson, J., Schertzer, D., & Lovejoy, S. (1991). Physically based modelling by multiplicative cascade processes. Non-linear variability in geophysics: Scaling and Fractals, 185-208.

Homepage