Extremes

Lesson

Introduction
Theory
Extreme value theory
Multifractal phase transition
- Introduction
- Bare and Dressed quantities
- First order phase transition
- Empirical power law estimation
To go further
Exercises
Conclusion

First order phase transition

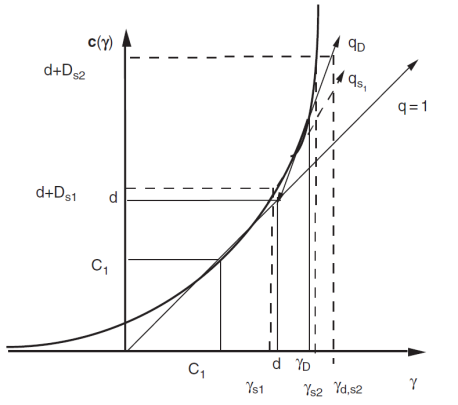
We now discuss the more violent first order transition which may occurs for a multifractal process that does not express all its variability at the observed scale. It has been shown in Schertzer et al, 1987^[1] that the integration of dressed quantity leads to statistical discrepancies ( ) as soon as the order of moments 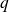becomes greater than a certain critical value defined by:

$K(q_D) = (q_D-1)D; \quad q_D > 1$

We can use the Legendre transform of the above equation to obtain the expression of the co-dimension function:

$c_D(\gamma) = q_D(\gamma- \gamma_D) + c(\gamma_D); \quad \gamma > \gamma_D$

The divergence of the moment of random variable 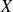( 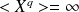for 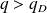) is the algebric fall of the probability distribution. The exponent of this tail probability, which characterizes the relative frequency of extreme events, is therefore nothing but the order of the critical statistical discrepancy; thus we have:

$P(X \geq s ) \approx s^{q_D} \Leftrightarrow <X^q> = \infty, \quad q \geq q_D$

Where is the threshold of intensity. This statistical behaviour is a consequence of the fact that the sum of the contributions is dominated by the contribution that is the strongest, that is, rare events have a dominant contribution.

Schematic diagram of c(γ), cd(γ) indicating two sampling dimensions DS1, DS2 and their corresponding sampling singularities γS1 < γD < γS2 < γd,S2; the critical tangent (slope qD) contains the point (D, D). Schertzer et al. (1993). | Information^[2]

Schematic diagram of c(γ), cd(γ) indicating two sampling dimensions DS1, DS2 and their corresponding sampling singularities γS1 < γD < γS2 < γd,S2; the critical tangent (slope qD) contains the point (D, D). Schertzer et al. (1993). | Information^[2]

Schertzer, D., & Lovejoy, S. [1987]
Schertzer, D., & Lovejoy, S. (1987). Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes. Journal of Geophysical Research: Atmospheres, 92(D8), 9693-9714.
Schertzer, D., & Lovejoy, S. (1993). Lecture notes: nonlinear variability in geophysics 3: scaling and mulitfractal processes in Geophysics. In NVAG3 Conference, CargÂese, Institut d'Etudes Scientifique de CargÂese, France (p. 292).

Homepage