Extremes

Lesson

Definition

The large deviation theory takes an interest of rare events and asymptotic calculation of their probabilities. At first sight it may seems rather formal, as we first give an intuitive idea of what it is the principle of large deviations. As an example, let 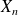be the average of independent and identically distributed random variables (iid) of Gaussian distribution. 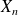follows a normal distribution of expectation 0 and variance so that for any interval A:

$P(\sqrt{n} X_n \in A) = \frac{1}{\sqrt{2 \pi}} \int_{A} e^{-x^2 /2} dx$

The typical value of 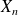is of order 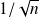. Let . The probability of the event 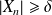tends to zero:

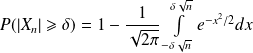
$P(| X_n | \geqslant \delta) = 1 - \frac{1}{\sqrt{2 \pi}} \int \limits_{-\delta \sqrt n}^{\delta \sqrt n} e^{-x^2 /2} dx$

Such that

$\frac{1}{n} \log P(| X_n | \geqslant \delta) \rightarrow - \frac{\delta^2}{2} \quad for \quad n \rightarrow + \infty$

Thus, with small probability, 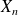deviate from its typical behavior taking a large values. This explains the terminology of "large deviation".

Homepage