Extremes

Lesson

Introduction
Theory
- Definition
- Coin tossing example
- Financial assets
Extreme value theory
Multifractal phase transition
To go further
Exercises
Conclusion

Coin tossing example

Let's start with a simple example: which is the distribution of N flips of coin tossing, we assign the value 0 for the heads and the value 1 for the tails.

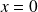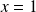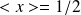Lets the value of one flip, we have with the probability and with the probability of . The random variable has the average and a standard deviation .

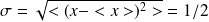It is easy to show that the partial average 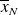of 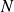independent flips of with :

$\overline{x}_N = \frac{1}{N} \sum \limits_{i=1}^{N} x_i$

admit a Gaussian distribution:

$P_{gauss} (\overline{x}_N) = \sqrt{\frac{2N}{\pi}}e^{-2N(x- 1/2)^2}$

The central limit theorem can provide more detailed information about the behavior of 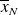However, the approximation by the central limit theorem may not be accurate if is far from 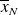. Also, it does not provide information about the convergence of the tail probabilities as 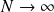. However, the large deviation theory can provide answers for such problems:

$P_{LD} (\overline{x}_N) = \sqrt{\frac{2N}{\pi}}e^{N(- \log(2)-(1-x) \log(1-x) -x \log(x) )}$

This expression can be deduced from Stirling formula for .

Homepage