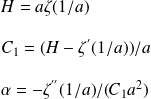Methods of Analysis

Lesson

Theoretical estimation

The different methods to estimation the UM parameters described above can be applied to a conservative field or flux (see Multiscale Analysis : Multfractal courses). However, directly observable quantities are rather the (vector) velocity field of temperature field which are a non-conservative quantities. Kolmogorov in [ Kolmogorov, 1941^[1]] proposed to characterize these processes by the analysis of their spatial/ or temporal increments. The statistical moments (in space) of these increments are the structure functions, defined by:

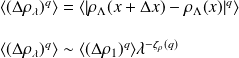
$\langle (\Delta \rho_\lambda)^q \rangle = \langle |\rho_\Lambda (x + \Delta x) - \rho_\Lambda (x ) |^q \rangle \\ \quad \\ \langle (\Delta \rho_\lambda)^q \rangle \sim \langle (\Delta \rho_1)^q \rangle \lambda^{-\zeta_\rho (q)}$

Illustrative diagram of the structure function exponent

Where the scalar field can be a passive scalar field (temperature), or one component of the velocity field. is the smallest resolution , 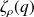is the scaling exponent of the structure function. Using the dimensional analysis the increments of the field has been related to those of related flux density :

$\Delta \rho_\lambda \sim \Big( F_\lambda \Big)^a \Big( \frac{L}{\lambda} \Big)^H$

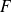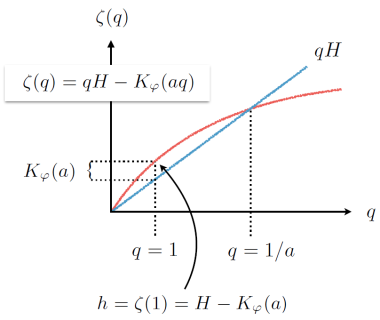
Using the above relation, the structure function scaling exponent can be expressed in the framework of UM as :

$\zeta_\rho (q) = qH - K_F(aq)$

The UM parameters can be calculated as follow :

$H = a \zeta(1/a) \\ \quad \\ C_{1} = (H - \zeta^{'}(1/a) ) /a\\ \quad\\ \alpha = - \zeta^{''} (1/a)/(C_{1} a^2 )$

[Kolmogorov, 1941]
Kolmogorov, A. N. (1941, January). The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In Dokl. Akad. Nauk SSSR (Vol. 30, No. 4, pp. 301-305).

Homepage