Universal multifractal model (UM)
According to cascade models introduced in the section Cascade Phenomenology, one can directly draw some parametric forms of the functions
and
for which the used parameters have a physical meaning. The number of parameters that can used is infinite, but according to the used probability distribution, we can observe different parametric forms of
.
Among the different probability distribution for the weights generation, the Levy distribution shows some "universality"
. The central limit theorem states that a sum of probability distribution converge to the Lévy distribution.
Schertzer and Lovejoy 1987, proposed a model with two parameters, which is a universal attractor under fairly general conditions for the process generated by multiplicative cascade, for which the logarithm of the weight
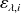follows a Lévy distribution. Adding the
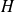parameter, the model can be applied to the non-conservative process.
For the universal mutifractal model, the statistical moment function has the following parametric from:
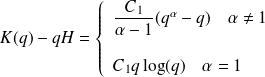
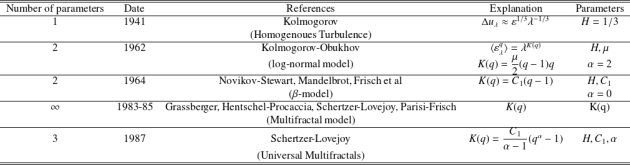
The following table summarizes some model and their required number of parameters:
