K(q) proprieties
The scale proprieties of the moment of order
obtained above, induce a specific behavior of the spectra energy obtained using the Fourier analysis in the frequency space (for time series). As we have seen in the previous module, the spectra is described using a power law:
Where
represent the energy spectra,
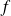is the frequency of the signal and
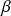is the spectra exponent.
The power spectra is characterized by the statistical order of
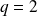in the Fourier space. The Wiener-Khintchine theorem shows that it corresponds to the Fourier transformation of the auto-correlation function of the time series.
A mentioned previously, the process can be described using two function
or
, then it is easy to go from a representation to another. The Mellin transformation which link the statistical moment of order
and the the probability function takes a simple shape in the multifractal framework. The functions
and
are related by the Legendre transformation as :
![K(q) = max_{\gamma}[q\gamma-c(\gamma)] \\ \quad\\ C(\gamma) = max_{q}[q\gamma-K(q)] \\](../res/eq12.png)
Looking for the maximum of
and
we can find :
This means that each singularity can be associated to the moment of order
and vice versa.
