Fractal

Lesson

Co-dimension

Let the Euclidean dimension in 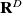, the support of the studied fractal set . If 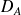is the fractal dimension of the object , we define de co-dimension of the fractal object

(Mandelbrot (1967) ; Mandelbrot (1977) ; Mandelbrot (1983) ; Barnsley (1988) ; Feder (1988) ; Falconer (1990)) as :

This co-dimension is a fundamental notion in the study of the fractal nature of the objects.

For instance, let 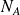the needed number of the box to overlap the space 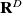, at the resolution (scale ratio) and the need one to overlap the fractal object at the same resolution of fractal dimension 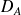. Using the box counting method we obtain :

$N_\lambda \approx \lambda^D \\ N_\lambda (A) \approx \lambda^D_A$

We can deduce :

$\frac{N_\lambda (A)}{N_\lambda } = \lambda^{D_A -D} = \lambda^{-C}$

being the co-dimension defined above. This formula is that of probability defined on the fractal set (Lovejoy et Schertzer (1992)). It reflects the probability that a cube in the ensemble 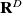at the resolution is contained in the fractal set .

Homepage