Von Koch snowflake
We can define geometric objects with fractal properties. This is the case of the Von Koch curve for which we propose an iterative construction (see figure below).

We start from straight segment of length
 (iteration 0). This segment is fractionated in three segments of length
(iteration 0). This segment is fractionated in three segments of length
 , then we construct an equilateral triangle taking as a basis the central segment. Finally, we remove the central segment used as a basis to the triangle. We thus obtain the first iteration, consisting of four segments of length
, then we construct an equilateral triangle taking as a basis the central segment. Finally, we remove the central segment used as a basis to the triangle. We thus obtain the first iteration, consisting of four segments of length
 . The second iteration will be obtained by repeating the above operation on each of the four segments obtained following the first iteration, and will continue indefinitely.
. The second iteration will be obtained by repeating the above operation on each of the four segments obtained following the first iteration, and will continue indefinitely.
If we look more to its length, studying the limit when
 tends to the infinity of the length of
tends to the infinity of the length of
 iteration:
iteration:
We can see that when
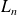 tends to the infinity with
tends to the infinity with
 until each iteration, the curve length is multiplied by
until each iteration, the curve length is multiplied by
 .
.
If we come back to the equation of overlapping of fractal object defined in the slide (Dimensions):
One can easily calculate the fractal dimension of the curve noting that :
 when
when
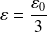 :
:





