Spectral Analysis

Data analysis

Data analysis

As shown in this lecture, the spectral analysis is used to identify the involved process, and also to chuck the propriety of scale invariance. In this exercise we use velocity data from JHU wind tunnel[1] to characterize the process.

Question

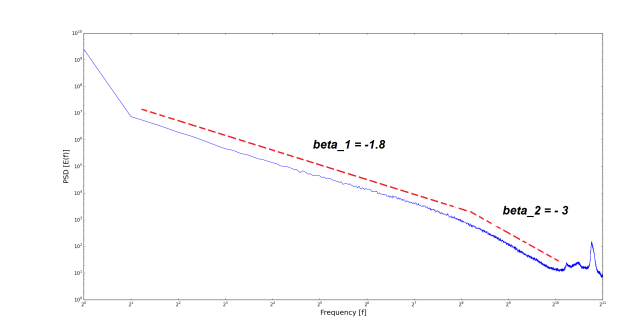
  • Unzip the data file and plot the corresponding PSD, divide the data sample into sub-samples of length 4096 points and perform the Fourier transform on each.

  • Compute the average spectrum and plot 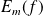, where 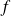is the frequency.

  • Check if there is scaling break and evaluate the spectral slope 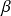on range if scale.

Solution
1
"""
2
@author: yacine.mezemate
3
"""
4
import numpy as np
5
import scipy as sp
6
import matplotlib.pylab as plt
7
8
#Load data
9
data = np.loadtxt('data.txt')
10
11
#Define length data
12
LenMax = data.shape[0]
13
SampleLenght = sp.power(2,12)
14
Nb = LenMax/SampleLenght
15
16
#Memory allocation
17
FMax=np.floor(SampleLenght/2)
18
f = sp.arange(1,FMax+1,1)
19
E = sp.zeros((FMax,Nb))
20
21
#Calculate the PSD for each sub-sample
22
for j in range(Nb-1):
23
    
24
    DataSample = data[SampleLenght*j:(j+1)*SampleLenght]
25
    Buffer = np.absolute(np.fft.fft(DataSample))
26
    E[:,j]=Buffer[0:FMax]*Buffer[0:FMax]
27
28
# Calculate the average PSD    
29
E_m = E.mean(1)
30
31
#Plot the average PSD
32
plt.loglog(f,E_m, basex =2)
33
plt.xlabel("Frequency [f]", fontsize = 18)
34
plt.ylabel("PSD [E(f)]", fontsize = 18)
35
36
# Calculate the slope for different range of scale
37
scale1 = 0
38
scale2 = 8
39
scale3 = []
40
41
if scale3 == []:
42
    rng = [sp.power(2,scale1),sp.power(2,scale2)]
43
else:    
44
    rng = [sp.power(2,scale1),sp.power(2,scale2), sp.power(2,scale3)]
45
    
46
rngLen = len(rng)
47
48
if rngLen ==2:
49
    Fmin = rng[0]
50
    Fmax = rng[1]
51
    slope = sp.polyfit(np.log2(f[Fmin:Fmax]),np.log2(E_m[Fmin:Fmax]),1)
52
    reg_lin=sp.poly1d(slope)
53
    beta1 = slope[0]
54
55
    print("beta 1 = "+ str(round(beta1,2)))
56
    
57
elif rngLen == 3:
58
    #beta 1    
59
    Fmin = rng[0]
60
    Fmax = rng[1]
61
    slope = sp.polyfit(np.log2(f[Fmin:Fmax]),np.log2(E_m[Fmin:Fmax]),1)
62
    reg_lin=sp.poly1d(slope)
63
    beta1 = slope[0]
64
    #beta 2
65
    Fmin = rng[1]
66
    Fmax = rng[2]
67
    slope = sp.polyfit(np.log2(f[Fmin:Fmax]),np.log2(E_m[Fmin:Fmax]),1)
68
    reg_lin=sp.poly1d(slope)
69
    beta2 = slope[0]
70
    
71
    print("beta 1 = " + str(round(beta1,2)), "beta 2 = " + str(round(beta2,2)))
72
PSD of wind velocity showing two scaling range with different value of beta
  1. Kang, H. S et al, [2003]
    Kang, H. S., Chester, S., & Meneveau, C. (2003). Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. Journal of Fluid Mechanics, 480, 129-160.
PreviousPreviousNextNext
HomepageHomepagePrintPrintCreated with Scenari (new window)