Spectral Analysis

Lesson

Introduction
Some definitions
- Definition
- Some applications
- Spectral analysis is based on Fast Fourier transform FFT
- Discrete Fourier transform DFT
Power spectral density (PSD)
Scaling analysis
Identification of some processes
Exercises
To go further
Conclusion

Spectral analysis is based on Fast Fourier transform FFT

Fourier analysis, is a way to decompose a signal into a sum of elementary signals, which have the propriety of being easy to analyse. The interest of this decomposition lies in the fact that the elementary signals are periodic and complex :

$S_e(t) = e^{j2 \pi ft} = cos(2 \pi ft) + j sin (2 \pi ft)$

Where f represent the frequency.

The Fourier transform or integral is the right tool for non-periodic functions. We convert from series to transform by imagining a system described by a continuum of “fundamental” frequencies.

Lets now imagine our function or signal 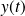expressed in terms of a continuous series of harmonics:

$y(t) = \int \limits_{- \infty}^{+ \infty} Y(f) \frac{e^{jft}}{\sqrt{2 \pi}} df$

The expansion amplitude 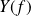is analogous to the Fourier coefficients 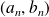and is called the Fourier transform of 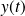. The above integral is the inverse transform since it converts the transform to the signal. The Fourier transform converts 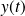to its transform :

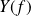$Y(f)= \int \limits_{- \infty}^{+ \infty} y(t) \frac{e^{-jft}}{\sqrt{2 \pi}} dt$

The 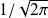factor in both these integrals is a common normalization in quantum mechanics but maybe not in engineering where only a single 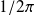factor is used. Likewise, the signs in the exponents are also conventions that do not matter as long as you maintain consistency.

The Fast Fourier Transform is an efficient implementation of the Discrete Fourier Transform (DFT). Of all discrete transforms, DFT is most widely used in signal processing.

Homepage