α-model
As we have seen in the previous exercise, the β-model is used to characterize the occurrence of a given field. However, in order to a have a complete characterization it is better to have the occurrence and the intensity of this field. As it has shown in this lecture, the α-model allows us to curry out this can of analysis.
Question
1 - According to the given elements in this lecture, give the expression of the singularities after n steps.
2 - What can be expect if we tend
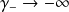
3 - Generate different field with different values of the parameter and comment the obtained results.
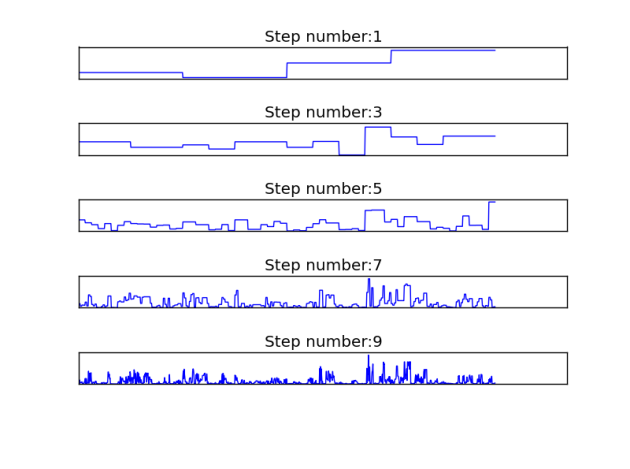
Solution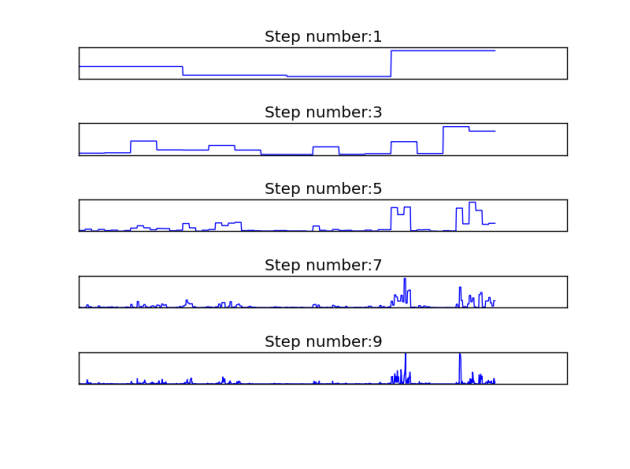
Different steps of field generation using α-model cascade with C = 0.2 and α = 1.1 
Different steps of field generation using α-model cascade with C = 0.8 and α = 1.7
1 - After n steps :
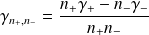with
2 - When
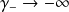we obtain the β-model.
1
# -*- coding: utf-8 -*-2
"""3
@author: yacine.mezemate4
"""5
import scipy as sp
6
from numpy import*
7
8
import matplotlib.pyplot as plt
9
from mpl_toolkits import mplot3d
10
11
######################## AlphaModel Function ##################################12
def AlphaModelCascade(alpha, C, Lambda, nsteps, dim):
13
alphaPrim = 1/(1-(1/alpha))
14
GammaPlus = C/alpha
15
GammaMinus = C/alphaPrim
16
17
if dim ==1:
18
19
resolution = sp.power(Lambda,nsteps)
20
data = sp.ones((resolution))
21
22
for n in range(nsteps):
23
24
LambdaMu = sp.power(Lambda,n+1)
25
Mu = random.uniform(0,1,LambdaMu)
26
Mu = Mu / sp.mean(Mu)
27
RangeList = range(0, resolution+1, resolution/LambdaMu)
28
29
for i in range(len(RangeList)-1):
30
31
rangeI = range(RangeList[i], RangeList[i+1])
32
33
if Mu[i] > sp.power(LambdaMu, GammaPlus):
34
35
data[rangeI]= Mu[i]*data[rangeI]
36
37
elif Mu[i] < sp.power(LambdaMu, GammaMinus):
38
39
data[rangeI] = Mu[i]*data[rangeI]
40
data = data
41
42
# Plot43
if n % 2:
44
plt.subplot(nsteps,1,n)
45
plt.plot(data)
46
plt.title("Step number:" + str(n))
47
frame = plt.gca()
48
frame.axes.get_xaxis().set_ticks([])
49
frame.axes.get_yaxis().set_ticks([])
50
51
52
if dim == 2:
53
54
resolution = sp.power(Lambda,nsteps)
55
data = sp.ones((resolution, resolution))
56
57
for n in range(nsteps):
58
59
LambdaMu = sp.power(Lambda,n+1)
60
Mu = random.uniform(0,1,LambdaMu)
61
Mu = Mu / sp.mean(Mu)
62
RangeList = range(0, resolution+1, resolution/LambdaMu)
63
64
for i in range(len(RangeList)-1):
65
66
for j in range(len(RangeList)-1):
67
68
rangeI = range(RangeList[i], RangeList[i+1])
69
rangeJ = range(RangeList[j], RangeList[j+1])
70
71
if Mu[i] > sp.power(LambdaMu, GammaPlus):
72
73
data[rangeI,rangeJ] = Mu[i]*data[rangeI,rangeJ]
74
75
elif Mu[i] < sp.power(LambdaMu, GammaMinus):
76
data[rangeI,rangeJ] = Mu[i]*data[rangeI,rangeJ]
77
78
return data
79
###############################################################################80
81
82
############################# Parameters ######################################83
alpha = 1.7
84
C = 0.8
85
nsteps = 10
86
Lambda = 2
87
dim = 1
88
89
############################# Cascade ######################################### 90
dataSim = AlphaModelCascade(alpha, C, Lambda, nsteps, dim)
91
92
