Cascade phenomenology

Lesson

Introduction
The matter of scale
Intermittency
Discrete cascade
Other type of cascade
- Introduction
- Auto-Similar spatial cascade
- Self-affine cascade
- Generalized scale invariance (GSI)
Exercises
To go further
Conclusion

Generalized scale invariance (GSI)

These type of cascades are defined by a linear operators with matrix which can be non-diagonal, unlike the previous type of cascade (defined above). In this approach, the general idea of GSI is to build up a family of structures 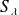defining vectors of generalized scale 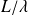. This can be done with the help of rather arbitrary unit ball 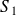and a generalized scale transform 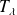that transforms the unit structure 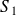into a structure reduced by a factor in scale.

The GSI matrix may have different shape, so the general expression can be :

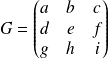
$G = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$

Shertzer and Lovejoy (1985) showed that the general expression of 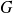seems to be constrained by the need to have specific values positive real part, in order to ensure a global contraction for and a global dilatation for .

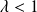A particular case of three dimension generator, is the one of spatio-temporal cascade which has the following diagonal matrix:

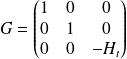
$G = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -H_t \end{pmatrix}$

It is a self-affine space-time cascade with two isotropic spatial direction and one time direction with anisotropic coefficient .

Homepage