Cascade phenomenology

Lesson

Introduction
The matter of scale
Intermittency
Discrete cascade
Other type of cascade
- Introduction
- Auto-Similar spatial cascade
- Self-affine cascade
- Generalized scale invariance (GSI)
Exercises
To go further
Conclusion

Self-affine cascade

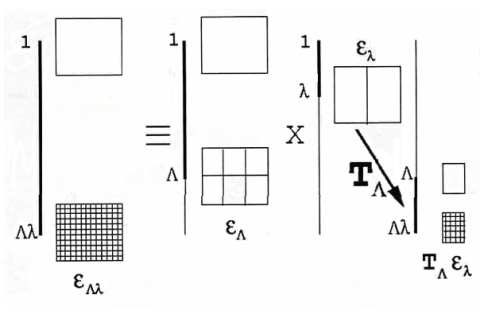
This the simplest case of non auto-similar generator, it has two invariant. The self-affine cascade are characterized by an anisotropy between two directions in space. If measure the gap compared to the isotropic scale law between two directions, the matrix 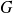is defined as :

$G = \begin{pmatrix} 1 & 0 \\ 0 & 1- H_{y} \end{pmatrix}$

is called the anisotropic exponent.

Self-affine cascade [from J.L Macor, 2007]

In order to get an self-affine cascade, we operate in two direction, a division by two number and 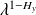. As we have seen above, the intensities are distributed following a random variable generator.

Homepage