Attractors
As we have seen dynamical systems are described by differential equations. The behavior of a given period of time is specified by the equation of a given dynamical system. The long period behavior of the systems is obtained by the integration of the equations either through analytical means or through iteration, often with the aid of computers. The dynamical systems arise from dissipative systems, their motion cease if there is no driving forces. The dissipation and the driving force tend to balance, killing off initial transients and settle the system into its typical behavior. The subset of the phase space of the dynamical system corresponding to the typical behavior is the attractor, also known as the attracting section. An attractor (or limit-set) is a set or a space to which a system evolves irreversibly in the absence of disturbances.
A strange attractor is a subset of points in the phase space that is fundamentally different to that of the objects belonging to ordinary Euclidean geometry; it is a geometric object characterized by a dimension that is not an integer number. Benoît Mandelbrot, also in the 1970s, coined the expression ‘fractal' to indicate geometric objects whose dimension is not integer62 (Mandelbrot, 1975): strange attractors are fractal objects.
As an example of strange attractors, we can mention the Lorenz attractor and Rössler attractor. The first one is probably the most famous example of a strange attractor, as well as being the first to be discovered. It describes the stability and the onset of convective or turbulent motion in a fluid heated from the bottom and cooled from the top. The system's equations are as follows:
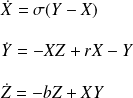
In which parameters
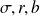have a specific meaning within the physical phenomenon that the model is aiming to describe. We return to this attractor in the exercises section.
The second example that we are going to illustrate is also very famous, and is the attractor obtained by Otto Rössler, who attempted to write the simplest example of a dynamical system featuring a chaotic attractor. The equations, which have a purely abstract meaning and are not intended for the modelling of any phenomenon whatsoever, are as follows:
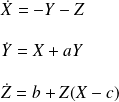
An illustration of this attractor has been given in the Poincar map section.
