Sensitivity to the initial condition
The sensitivity of chaotic systems to initial conditions is particularly well known under the moniker of the “butterfly effect,” which is a metaphorical illustration of the chaotic nature of the weather system in which “a flap of a butterfly's wings in Brazil could set off a tornado in Texas.” The meaning of this expression is that, in a chaotic system, a small perturbation could eventually cause very large-scale difference in the long run. The below figure shows the sensitivity of non-linear dynamical system to the initial condition. The behavior of the system is described by the following equation:
We fix the parameter
and run the system for
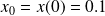and
.
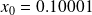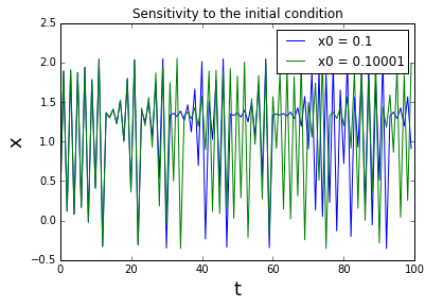
The two simulations are fairly similar for the first several steps, because the system is fully deterministic (this is why weather forecasts for just a few days work pretty well). But the “flap of the butterfly's wings” (the 0.00001 difference) grows eventually so big that it separates the long-term fates of the two simulation runs. Such extreme sensitivity of chaotic systems makes it practically impossible for us to predict exactly their long-term behaviors (this is why there are no two-month weather forecasts.
