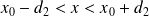Source Of Complexity

Lesson

Introduction
Matter of scale
Variability
Non-linearity
Introduction to differential equations
- What is a differential equation
- Classification of PDEs
- Existence and Uniqueness
Governing equations
Different approaches
Exercises
To go further
Conclusion

Existence and Uniqueness

When we deal with differential equations we are facing the problem of existence and uniqueness of the solution. In order to highlight these mathematical behavior, lets use the first order ODEs sush as:

$y^{'} = F(x,y), \quad \quad \quad y(x_0) = y_0 \quad \quad \quad (*)$

In order to answer the questions of existence and uniqueness, we relies on the following theorems:

Theorem 1 (Existence). Suppose that F(x,y) is a continuous function defined in some region:

containing the point 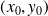. Then there exists a number of 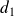so that a solution to 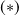is defined for

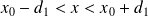
Theorem 2 (Uniqueness). suppose that both and 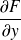are continuous functions defined in a region (see below) as in Theorem 1. Then there exists a number so that the solution to 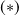, whose existence was guaranteed by Theorem 1, is the unique solution to 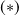for

Homepage