First order phase transition
The divergent statistical behavior indeed corresponds to the fact that rare and catastrophic events will make dominant contributions. In cascades, the flux energy is maintained by instabilities of all intensities. The transition from soft to hard processes corresponds to the fact that microscopic activity cannot be removed to yield a purely macroscopic description of the system. In this exercise we use velocity data from geophysical environment (lake) to illustrate the first order phase transition and the calculation of
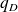. As we sad in the previous lectures, the velocity field can be generated according to the cascade phenomenology.
Question
Download the given data and load it in your work directory.
Calculate the following statistics : mean, variance and standard deviation.
Sort the negative values of the data and calculate their probability according to Weibull distribution
Plot in log-log the Pdf Vs the observation and estimate the
.
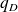# -*- coding: utf-8 -*-"""@author: yacine.mezemate"""import numpy as np
import matplotlib.pyplot as plt
########################### Data ################################Import datadata = np.genfromtxt("dataQd.txt", delimiter= '')
data = np.diff(data) # use the difference
plt.figure(0)
plt.plot(data)
plt.title("Data sample", fontsize = 18)
plt.ylabel("$\Delta v$", fontsize=16)
plt.xlabel("$time$", fontsize=16)
plt.show()
############################# Statistics ########################mu = np.mean(data) # mean
Var = np.var(data) # variance
std = np.sqrt(Var) # standard deviation
############################# Pdf calculation #################### Calculate and plot the Empirical PDF using Weibull distributionneg = abs(np.sort(data[data<0])) # sort negative values
P_neg = np.arange(len(neg), dtype = np.double)/len(neg) # probability of negative values
x = np.log(neg)
y = np.log(P_neg)
############################# qd calculation #####################Qdpoly = np.polyfit(x[1:1000], y[1:1000],1)
test = np.poly1d(poly)
############################# plots ##############################plt.figure(1)
plt.plot(x, y, marker='+', label ="Empirical Estimation") # plot PDF
plt.plot([x[1],x[1000]], [test(x[1]),test(x[1000])], lw = 6, label= "qd="+str(poly[0]))
# Plot informationsplt.legend(loc="down left")
plt.title("Probability distribution", fontsize = 18)
plt.ylabel("$\log(Pr(\Delta v))$", fontsize=16)
plt.xlabel("$\log(\Delta v)$", fontsize=16)
plt.show()
