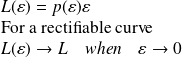Fractal

Lesson

Fractal concept

The fractals concept have been widely studied since their introduction by Benoît Mandelbrot(1975) in several developments and applications, which we try to give an overview. Nowadays, many researchers use them in a context far beyond the geometric aspect of their debut. Start with some fractal geometry elements seems appropriate, however, from a historical and educational point of view of all, but also from a practical point of view because geophysicist also has to solve geometric problems.

The curves we are used (lines, circles, ellipses, etc.) are rectifiable, which means that we are able to assign a length to any arc defined by two points such curves. Strictly speaking, this means that if we call 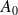and 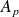respectively the origin and the end of this arc, we choose 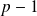consecutive points between these two points, realizing and a polygonal approximation of the arc studied.

Polygonal approximation of an arc of curve

The length of the polygonal approximation :

$L = A_{0}A_{1} + A_{1}A_{2} + .... +A_{p-1}$

tends to a finite limit, which will be the length of the arc studied simultaneously when p increases indefinitely, and that the length of the elementary segments 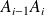tends to zero.

If we ensure that basic segment 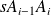are equal, their length then being equal to , that can be interpreted as a measuring gauge,

we will need to such segments to achieve the polygonal approximation and its length will be equal to:

$L(\varepsilon) = p(\varepsilon) \varepsilon \\ \text{For a rectifiable curve} \\ L(\varepsilon) \rightarrow L \quad when \quad \varepsilon \rightarrow 0$

Homepage